④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。四角錐台の体積の公式について。 この画像のように上下面が共に長方形、BC//FG 及び CD//GHとする四角錐台の体積が h/6(XyxY2(XYxy)) となる事を証明したいです。 この公式になるまでの説明と経緯を教えて下さい。 宜しくお願いします。正四角錐(せいしかくすい) 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交

正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ
四角錐 体積 公式
四角錐 体積 公式-直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!


問題 点pが動く四角錐の体積を求める 空間図形 数塾ブログ
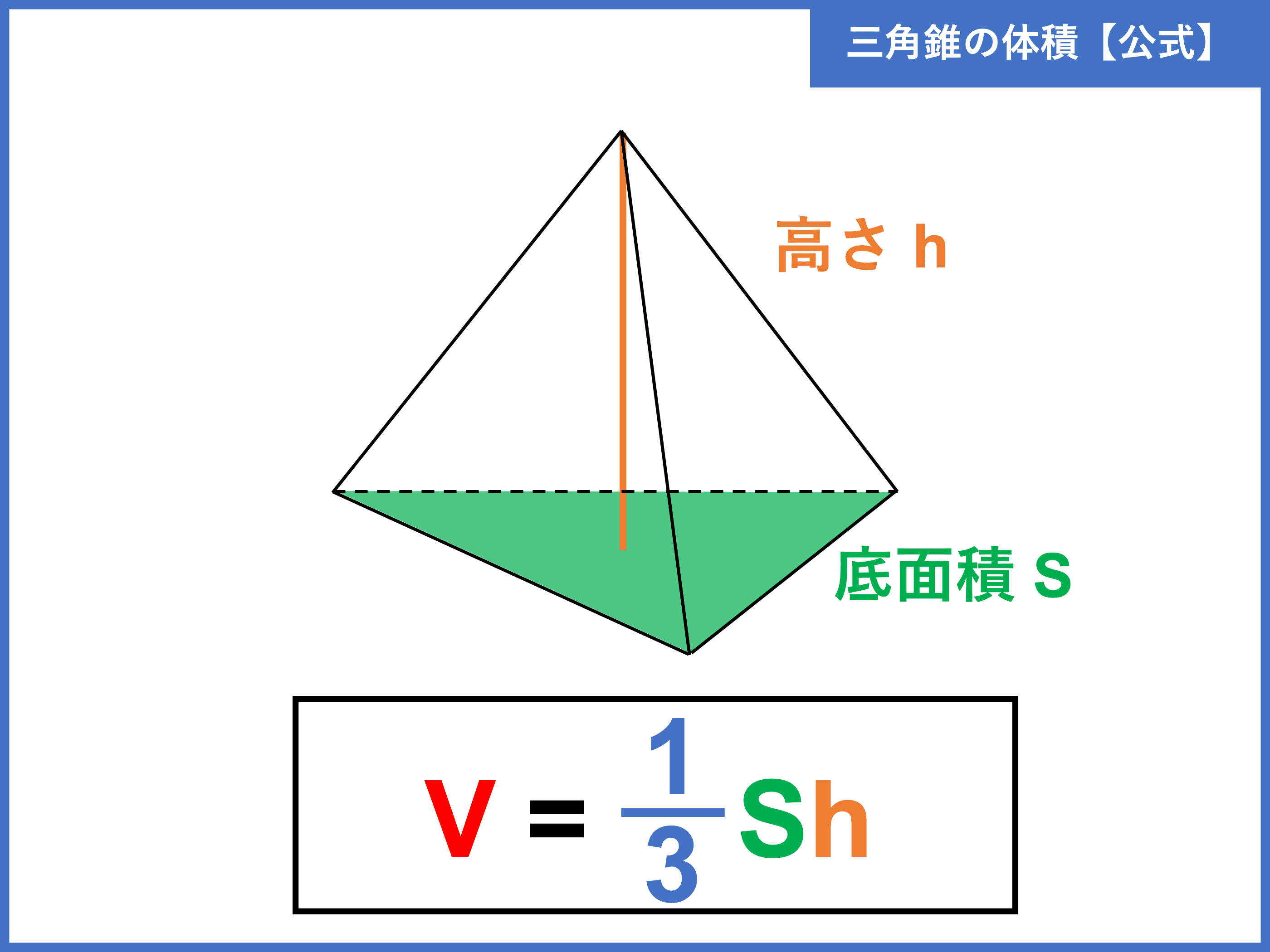
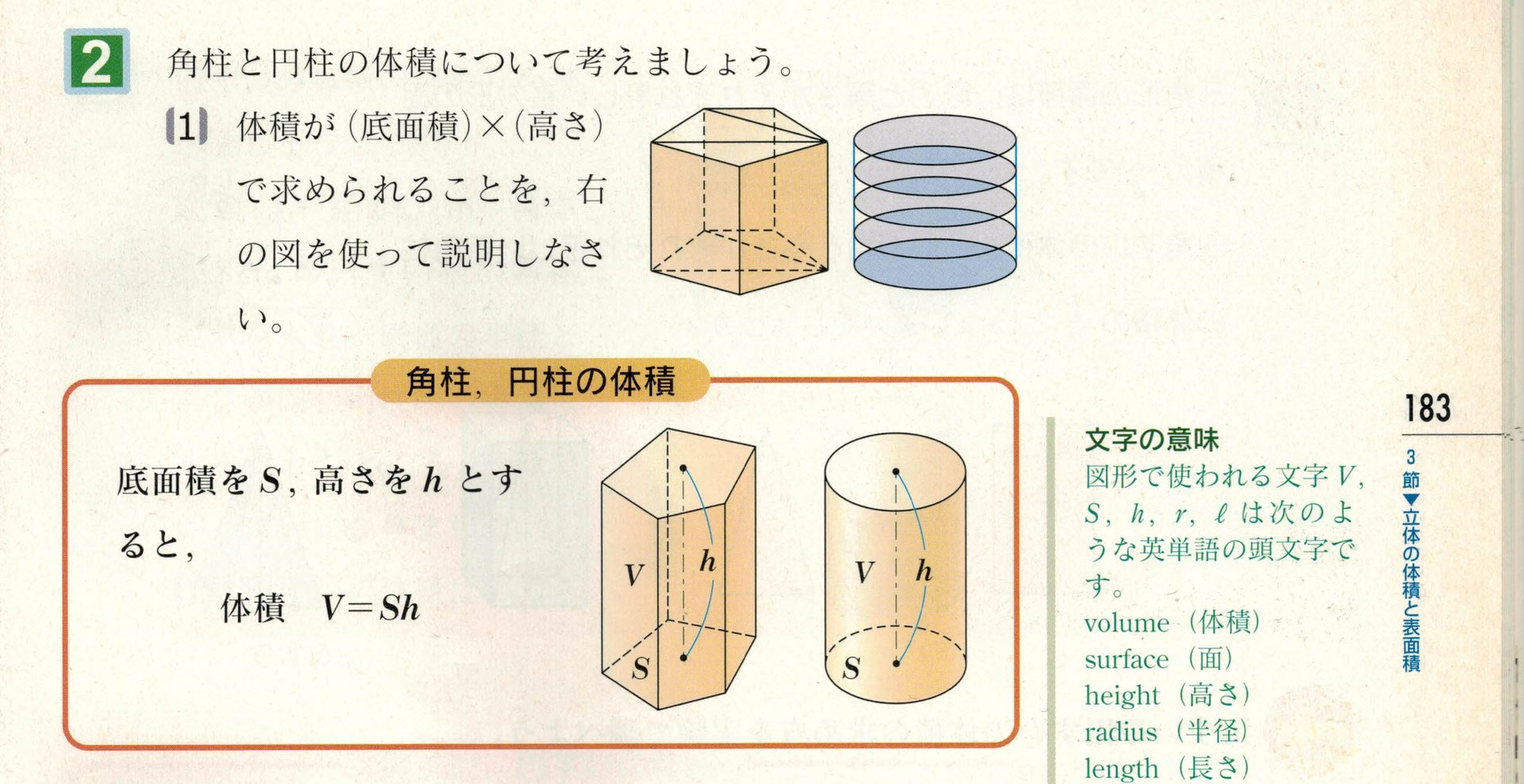
そのような四角錐の体積vを数式では以下のように表せれるだろう。 V = 1 3 a 3 × b a × c a = 1 3 a b c では頂点の位置が、底面のどの辺に対してもずれているような四角錐はどうかというと、四角錐の頂点を動かしても、それを構成するいくつもの断角錐・円錐の体積と表面積の公式 管理人 2月 5, 19 / 2月 15, 19 主に柱体(角柱・円柱)、錐体(角錐・円錐)、球の3種類の立体です。角錐や円錐の体積の公式はこれと似ています。同じように、底面積と高さを掛けます。その後、 3分の1にすることで体積が出ます。 つまり、角錐と円錐の体積を出す公式は以下のようになります。 角錐・円錐の体積 = 底面積 × 高さ × $\displaystyle\frac{1}{3}$
四角錐 ⇒ (上底下底)÷2×高さ×四角柱の高さ÷3 三角錐 ⇒ 底辺×高さ÷2×三角柱の高さ÷3 体積の求め方、覚え方 体積の公式の覚え方は簡単です。球の体積を除けば、たった2つの公式を覚えるだけで済むからです。長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。体積の公式、円形の面積の求め方は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 四角錐 ⇒ (上底下底)÷2×高さ
ある体積V 1を 有する三角正四角錐があると仮定する。 それに相似なピラミッドを最初のものよりも3倍小さい体積にするためには、この図のサイズを何倍に縮小すればよいでしょうか。 元の正角錐の公式を書くことによって、問題を解決し始めます。四角錐を平面で切った立体の体積比は (向かい合う1組の辺比の積) x (もう1組の辺比の平均) になるようです でも、これは底面が平行四辺形以上の特殊な場合でないと使えないし、そもそも四角錐を縦に切る作業がわかってしまえば面倒でもないので意味なし直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の



Nams出版プロジェクト 錐体の体積がなぜ1 3 3分の1 かを感覚的に納得させる方法



空間ベクトル 高校数学に関する質問 勉強質問サイト
長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。四角錐台の体積を計算する必要がありました。 上記公式に数字を当てはめるとA=43 B=36 a=29 b=19 h=18 単位cmです。 公式に当てはめて計算してみると大方18リットル=10升=?斗であることがわかりました。④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。
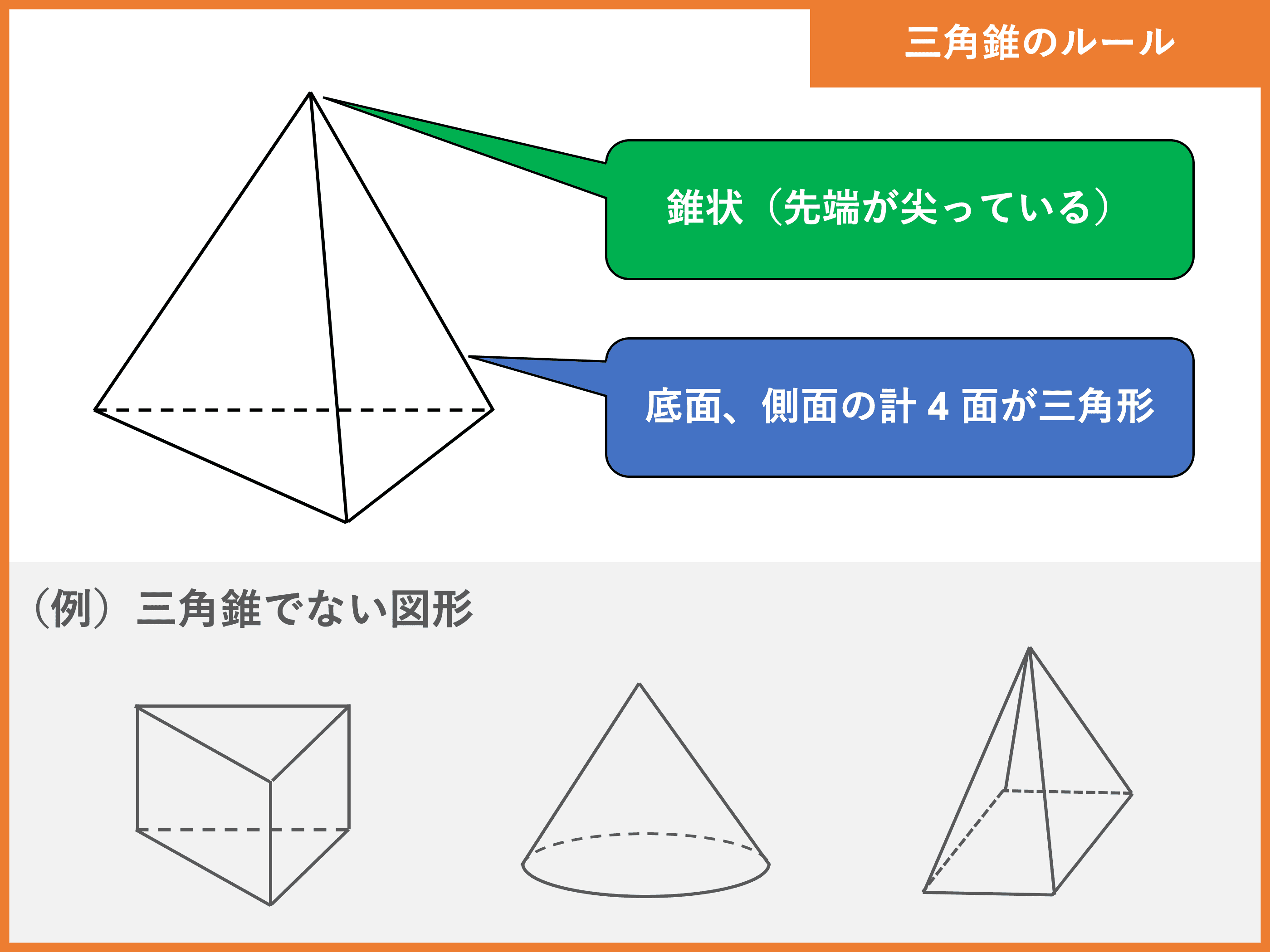


三角錐とは 体積 表面積の公式や求め方 受験辞典



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
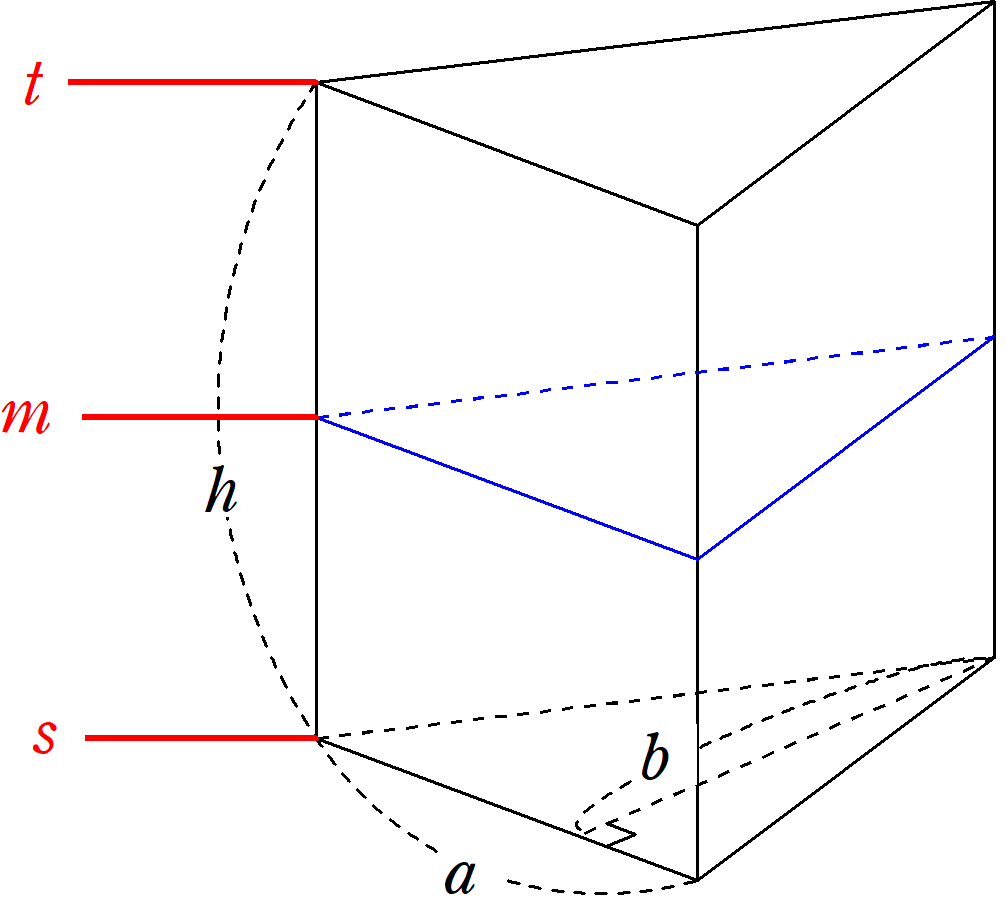
正四角錐(せいしかくすい) 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!



四角錐台の斜辺の長さ Okwave
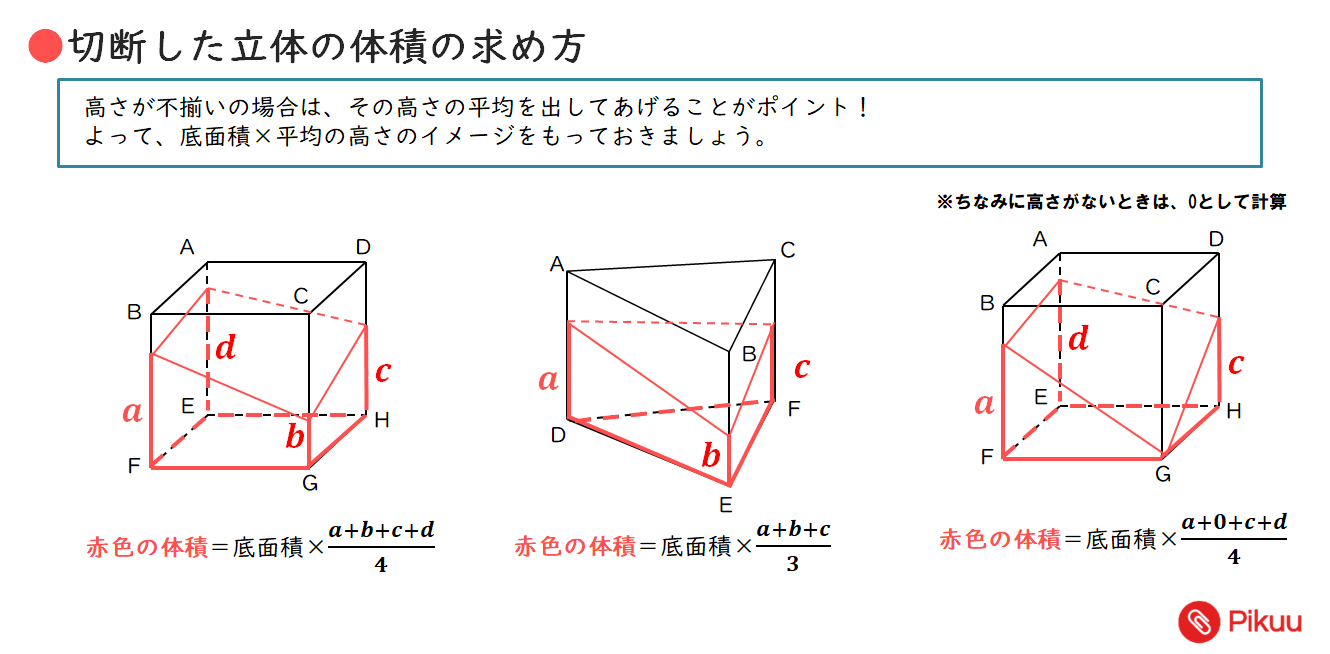


切断した立体の体積の求める練習問題 Pikuu
正四角錐の内接円の公式で 正四角錐出なくても使えますか? abcの1辺を2とする正三角形でoabcの四面体に内接する球の半径を求めよoa=ob=oc=4とする。公式通りなら表面積 abc=√3 oabシンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の



解き方教えてください Clear



この答えを見て いまいち意味がわかりません どうにか Clear
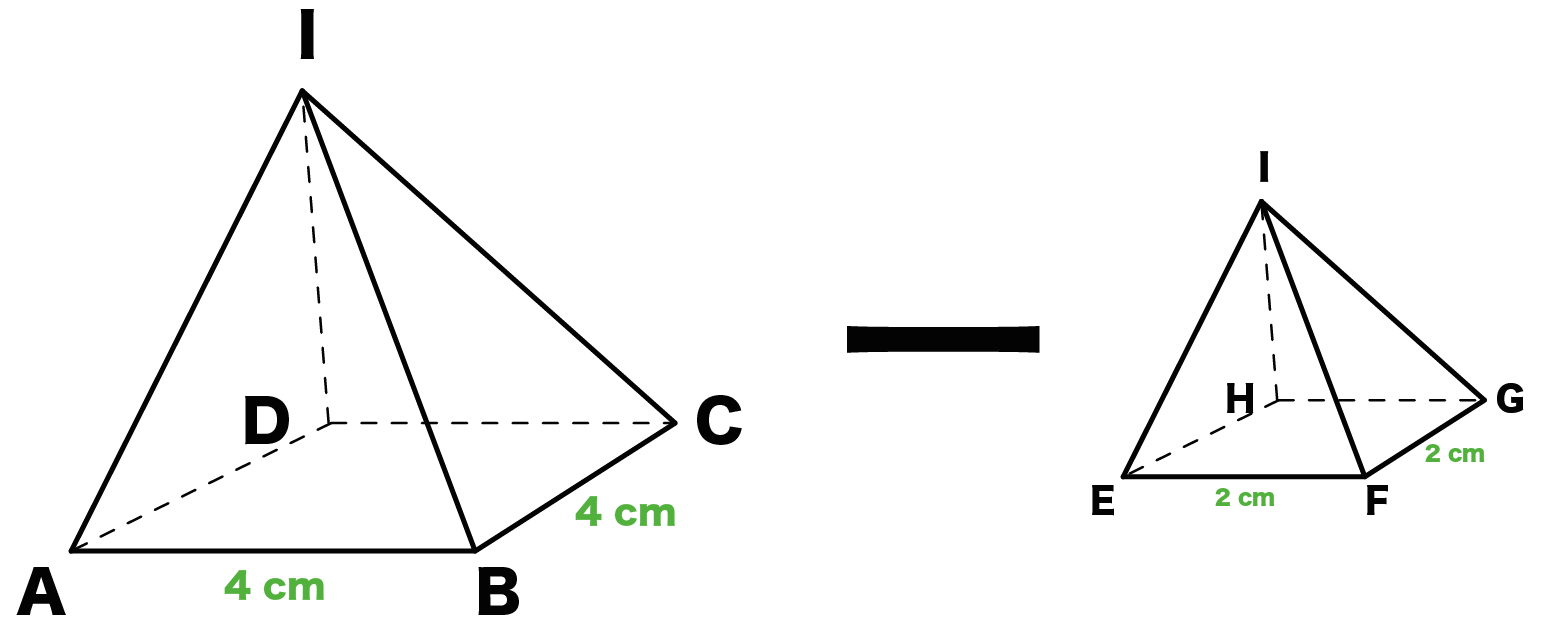
長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。正四角錐bdegの体積は,立方体abcdefghから,合同な4つの四角錐の体積を引くことで求められる。aを用いて,立方体abcdefghの体積は, ア cm3と表せ,四角錐abceの体積は, イ cm3と表せる。体積の公式、円形の面積の求め方は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 四角錐 ⇒ (上底下底)÷2×高さ
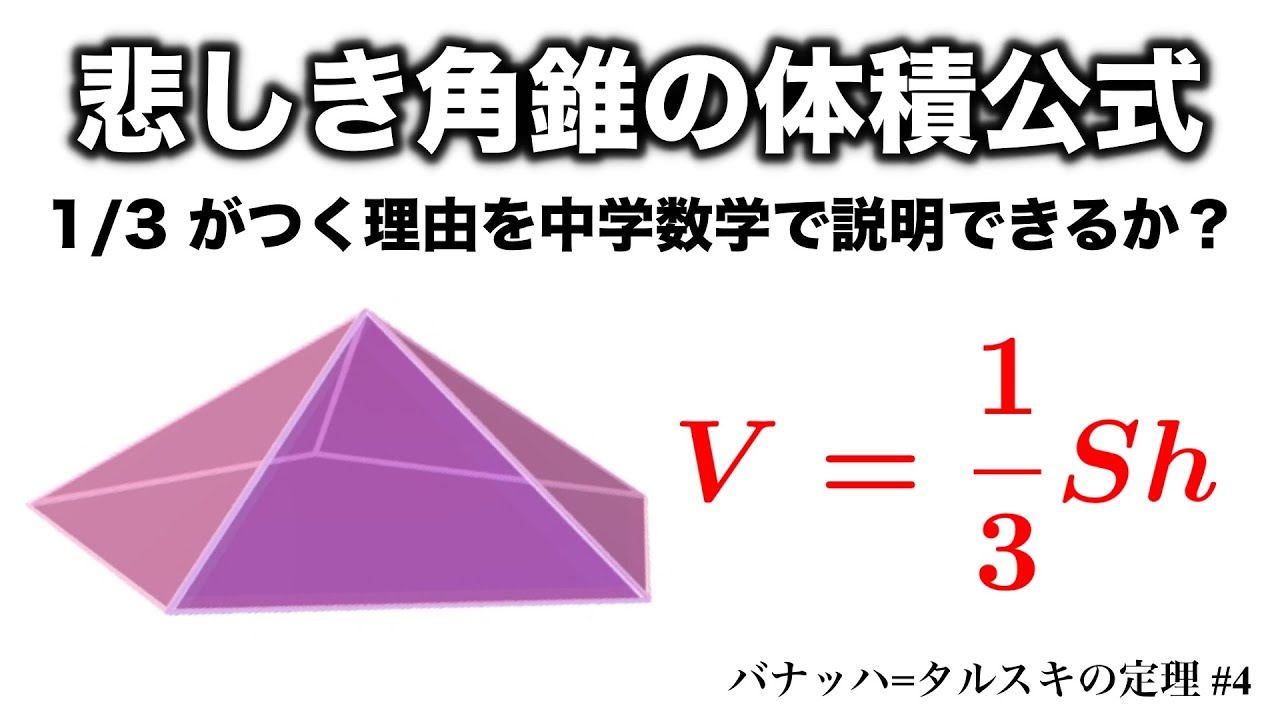


悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube



Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703
正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。四角錐台の体積の公式について。 この画像のように上下面が共に長方形、BC//FG 及び CD//GHとする四角錐台の体積が h/6(XyxY2(XYxy)) となる事を証明したいです。 この公式になるまでの説明と経緯を教えて下さい。 宜しくお願いします。三角錐 四角錐 円錐 三角柱 四角柱 円柱の底面積と体積の求め方を教えてください。 数学 正四角錐の体積について 正四角錐の体積は、 1/3×底面積×高さ ですが、 正四面体の体積 ルート2/12×a3乗のように正四角錐の体積叉は高さを 簡単に求めることはでき



数学 青チャートa 例題101 正四角錐の高さ 高校数学に関する質問 勉強質問サイト
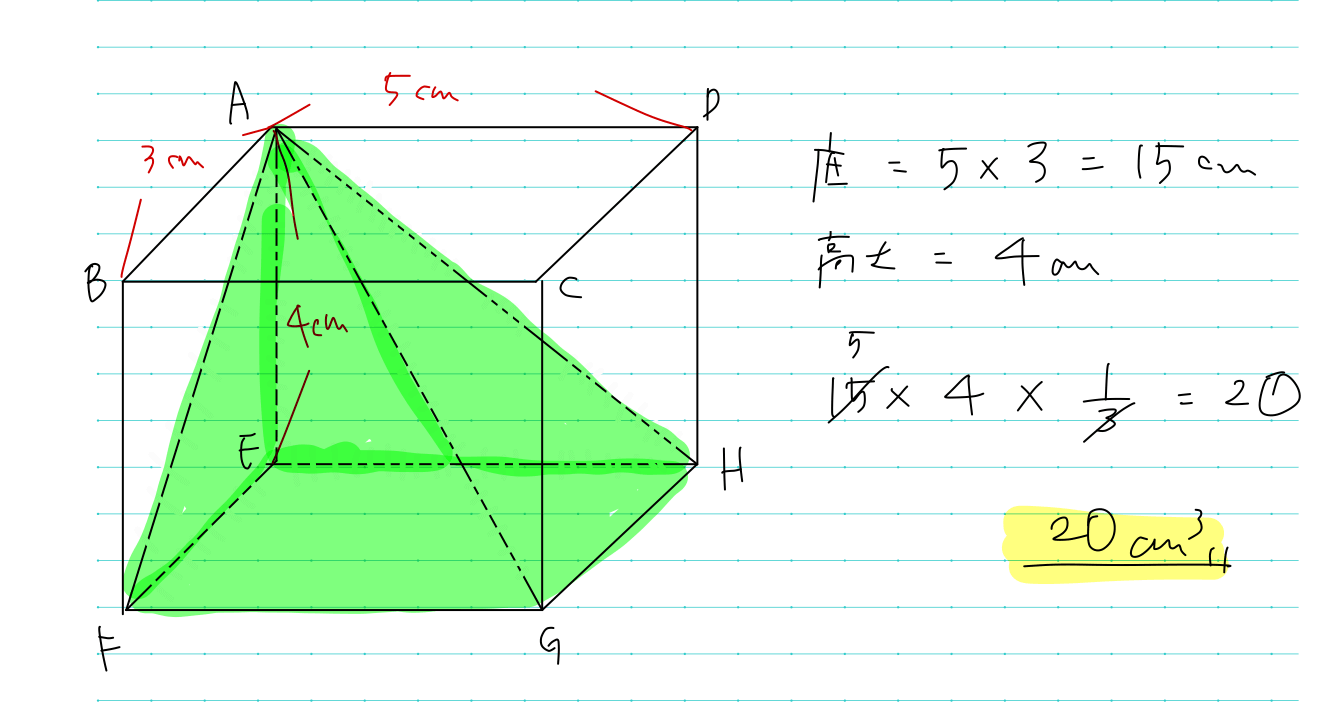


中2生用の北辰過去問を解いてみた 大問2 個太郎塾ふじみ野教室
長方錐の底面の横の長さを a, 縦の長さを b, 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。 直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当な直交変換により、以下の方程式に変換できる。


2



角錐 円錐の体積 Youtube
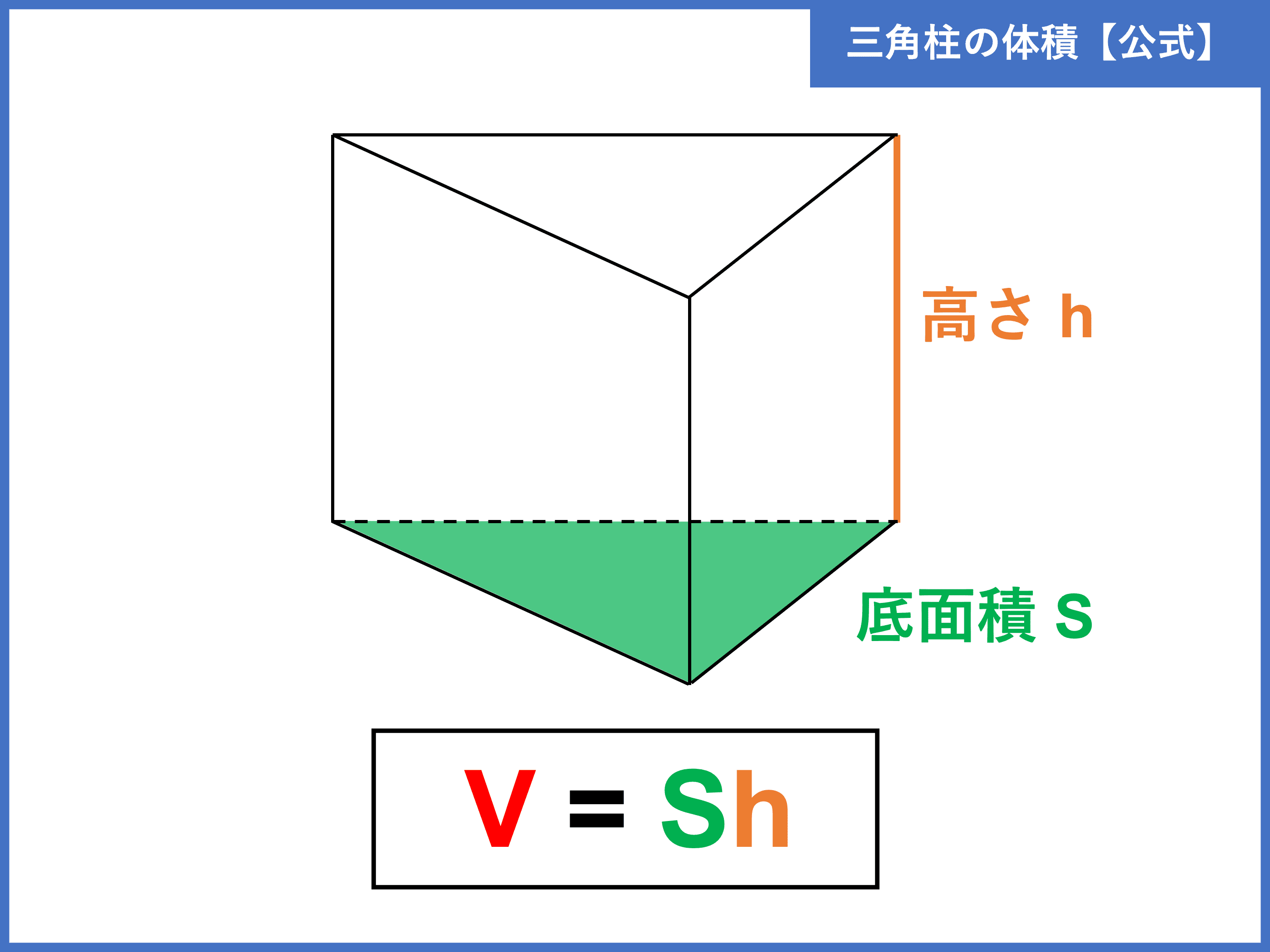


最高 50 三角柱 の 体積 公式 壁紙 配布


2



56 四角錐の切断と体積 Youtube


Core Ac Uk Download Pdf Pdf



この問題の解説の途中式の四角錐の体積を求めているところで 10 6 6 4とい Clear
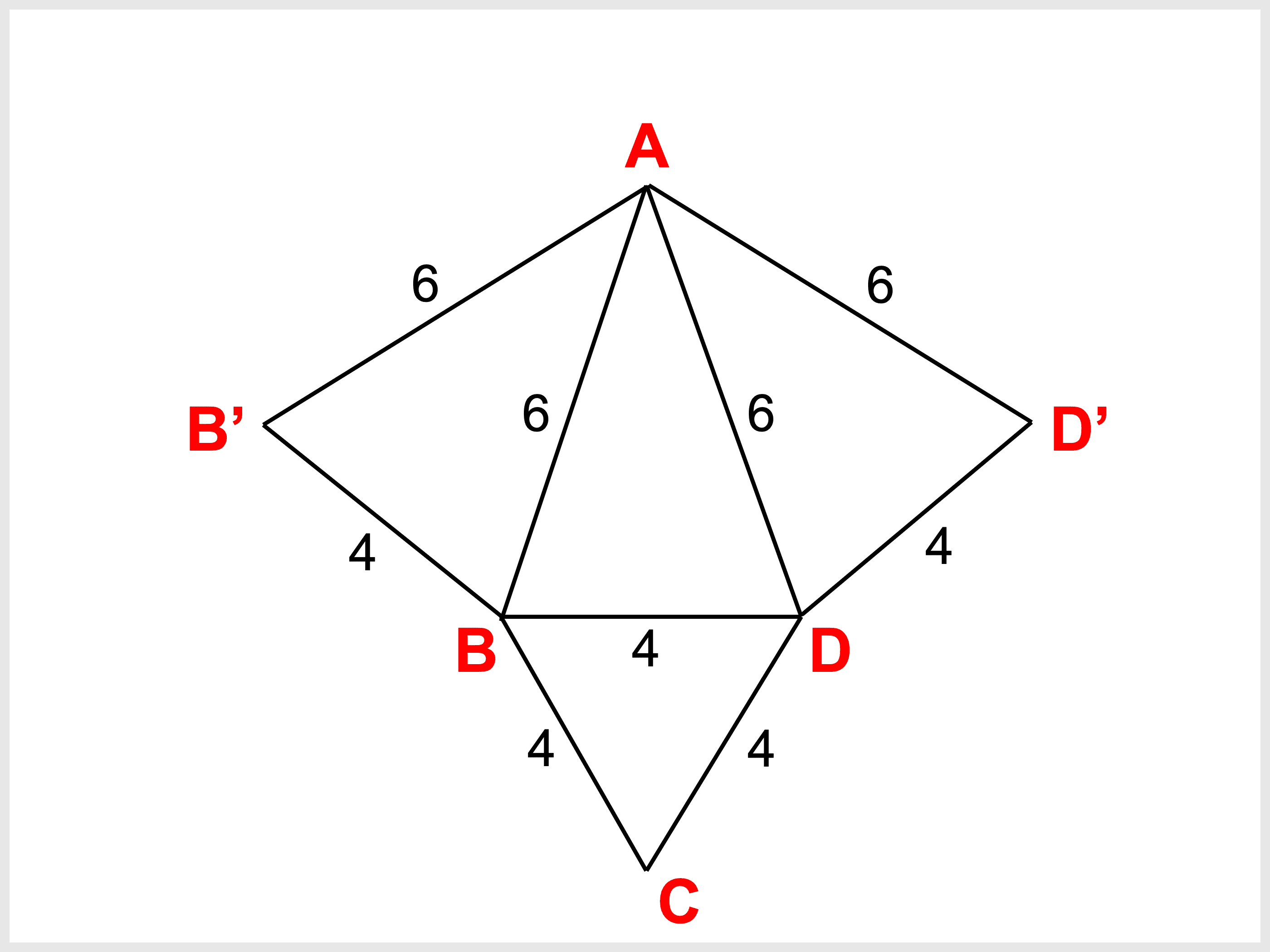


新しい 四 角錐 展開 図 書き方 アマゾンブックのポスト



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


2
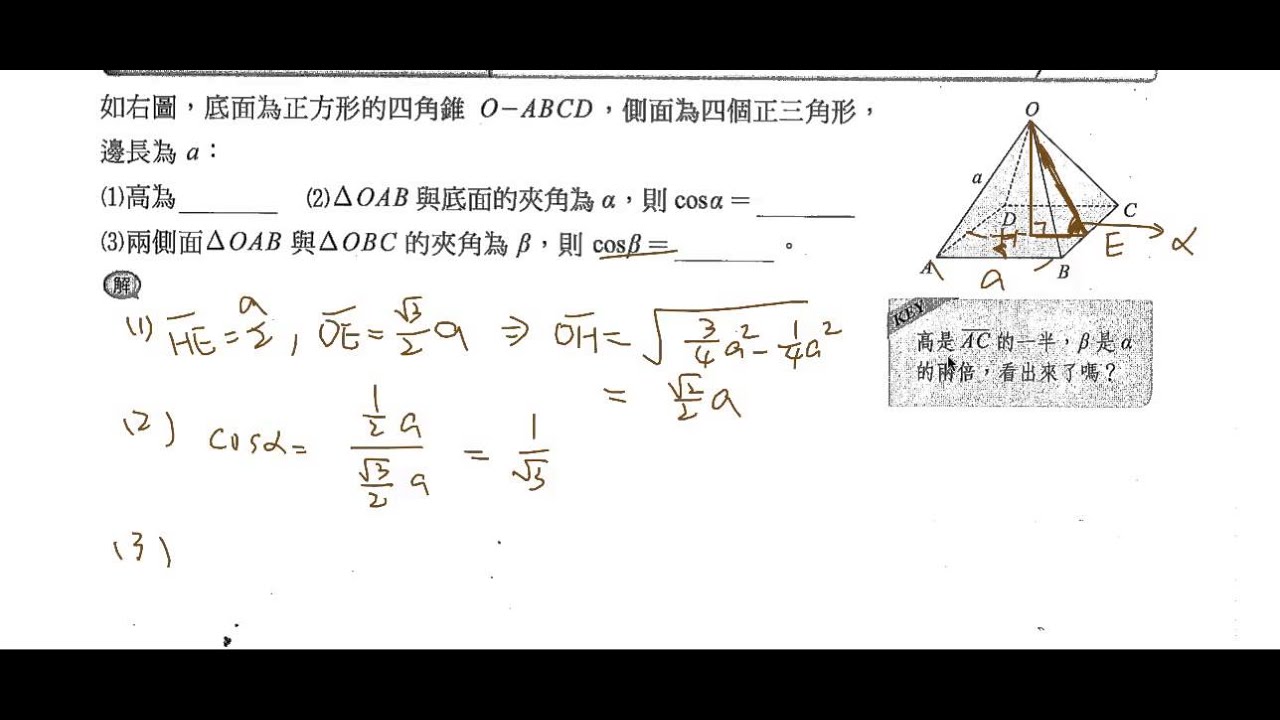


美しい 正四 角錐 体積 公式 壁紙 配布



表面積の比と体積の比 中学数学に関する質問 勉強質問サイト



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



正四角錐o Abcdの体積をvとして 四角錐o Pqrsの体積が Clear


様々な画像 最高 Ever 角錐 台 体積



簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



50 グレア 四角錐面積 壁紙配布



角錐體積公式的由來 Youtube



正八面体と球 Okwave



Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703



どうして1 3なの 錐の体積の公式の求め方 まなべーと


高校入試 数学 19年度 筑波大学附属駒場高校 空間図形 の 解説 後半 です 3つの動点を通る平面でできる切り口を底面とする四角錐の体積を求めます Youtube



生四角錐の表面積の求め方を教えてください 公式だけでもいいので Clear


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


2



錐体の表面積1 例1正四角錐の表面積の求め方 Youtube
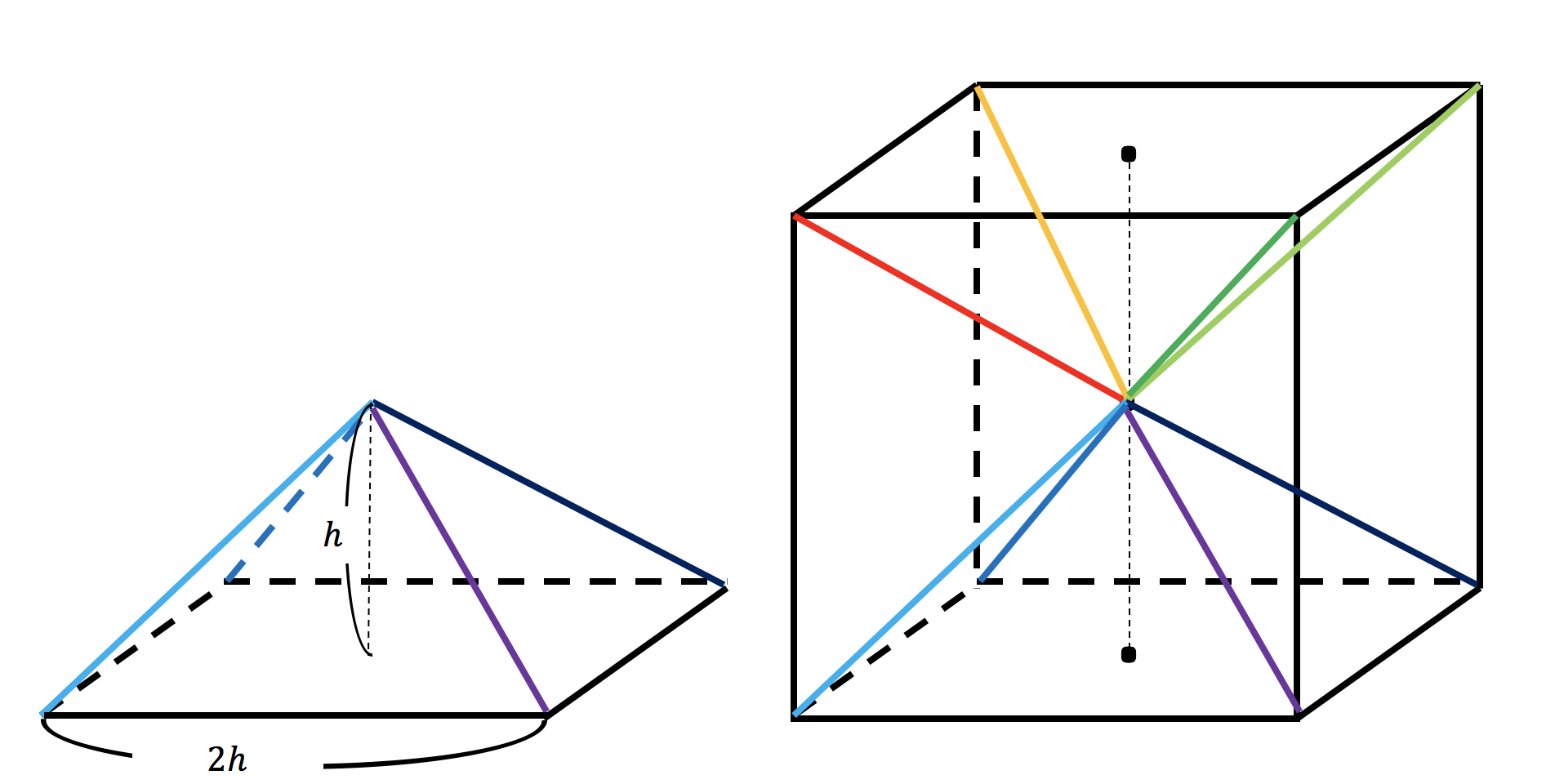


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



โน ตของ 体積 表面積 側面積 の公式 ช น Junior Clear



正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ
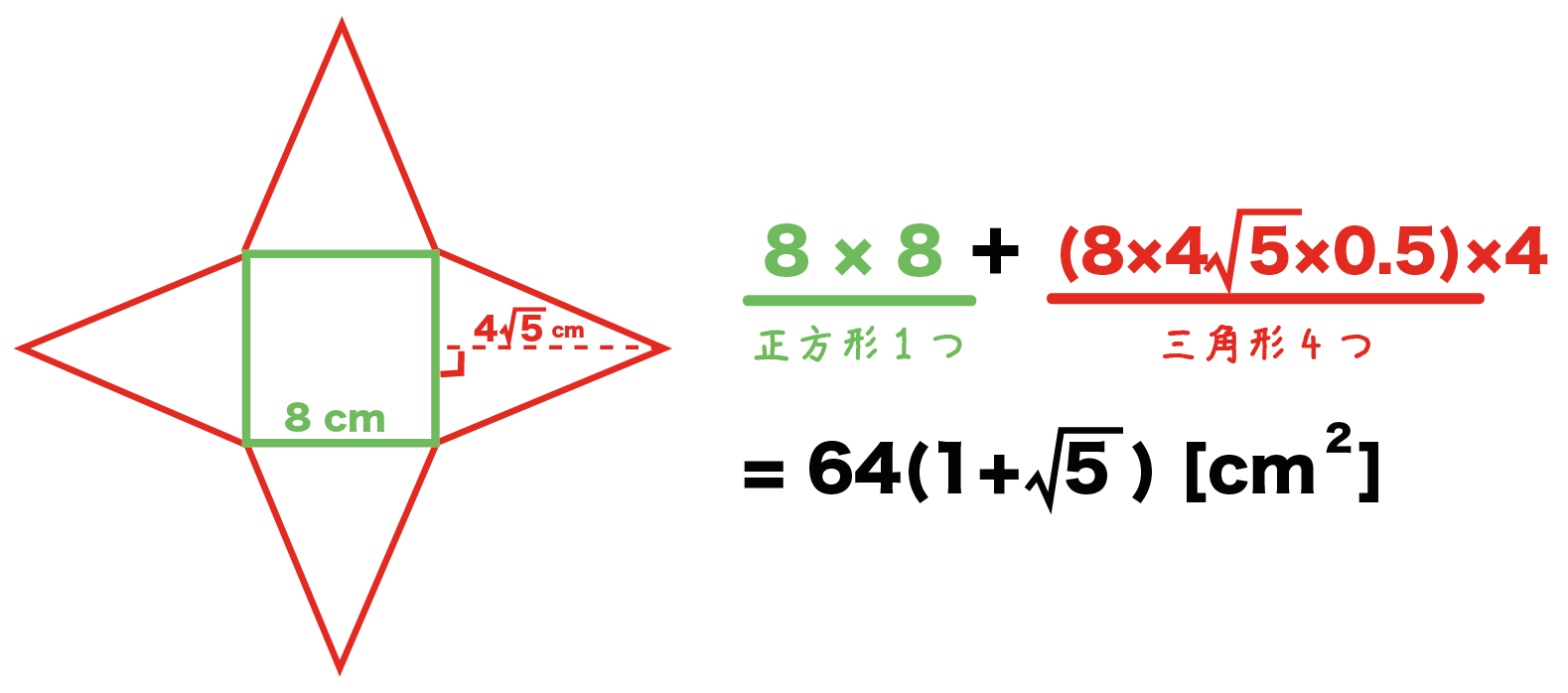


美しい 正四 角錐 体積 公式 壁紙 配布


2


簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 ねじれの位置の意味とは 角柱 角錐のどこ 問題を使って解説するぞ 数スタ



高校数学b ベクトルの外積 裏技 による法線ベクトル 空間の三角形の面積 平行六面体の体積 四面体の体積 受験の月



角錐の高さと体積 まなびの学園


立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者



高校数学 対称面をもつ四面体の体積 受験の月



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703


Core Ac Uk Download Pdf Pdf


Www Mext Go Jp Component A Menu Education Micro Detail Icsfiles Afieldfile 15 10 06 010 Pdf



数学中2 立体の体積と表面積 公式 中学生 数学のノート Clear


問題 点pが動く四角錐の体積を求める 空間図形 数塾ブログ



壁紙押入れ ロイヤリティフリー角錐体積公式



多角柱 円柱の体積 チーム エン


三角錐とは 体積 表面積の公式や求め方 受験辞典



数学3 高校数学に関する質問 勉強質問サイト



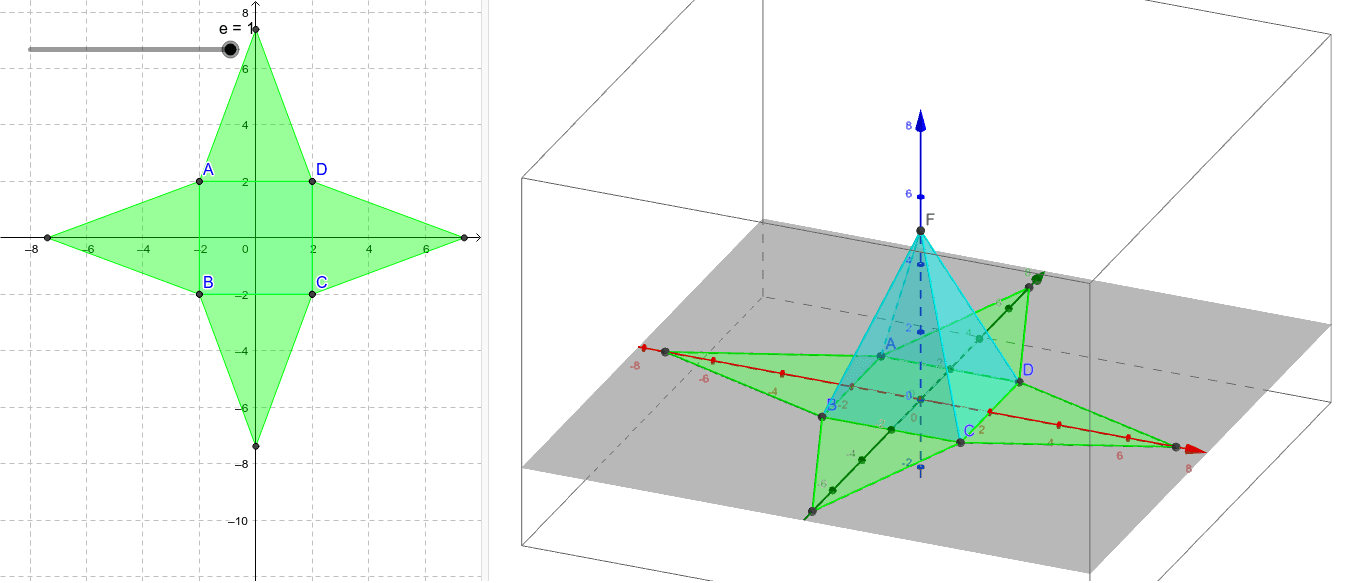
佐久間 今年の東大理系数学の第2問の3次元バージョンを作ってみました 次元が上がっている分 元の東大の問題より難しくなっていますが 三角柱と三角錐と四角錐の体積の公式しか使わないので 空間認識能力が高ければ小学生でも解けます



ヤフオク 数学史 数学5000年の歩み 中村滋 室井和男



正四面体について 高校数学に関する質問 勉強質問サイト



中学1年生 柱体 錐体の体積 公式 個別進学教室マナラボ受験 教育情報サイト


イメージカタログ フレッシュ 四 角錐 展開 図 書き方


Http Www Kurims Kyoto U Ac Jp Kyodo Kokyuroku Contents Pdf 1392 8 Pdf


悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube



正四角錐の問題 高校数学に関する質問 勉強質問サイト



高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月
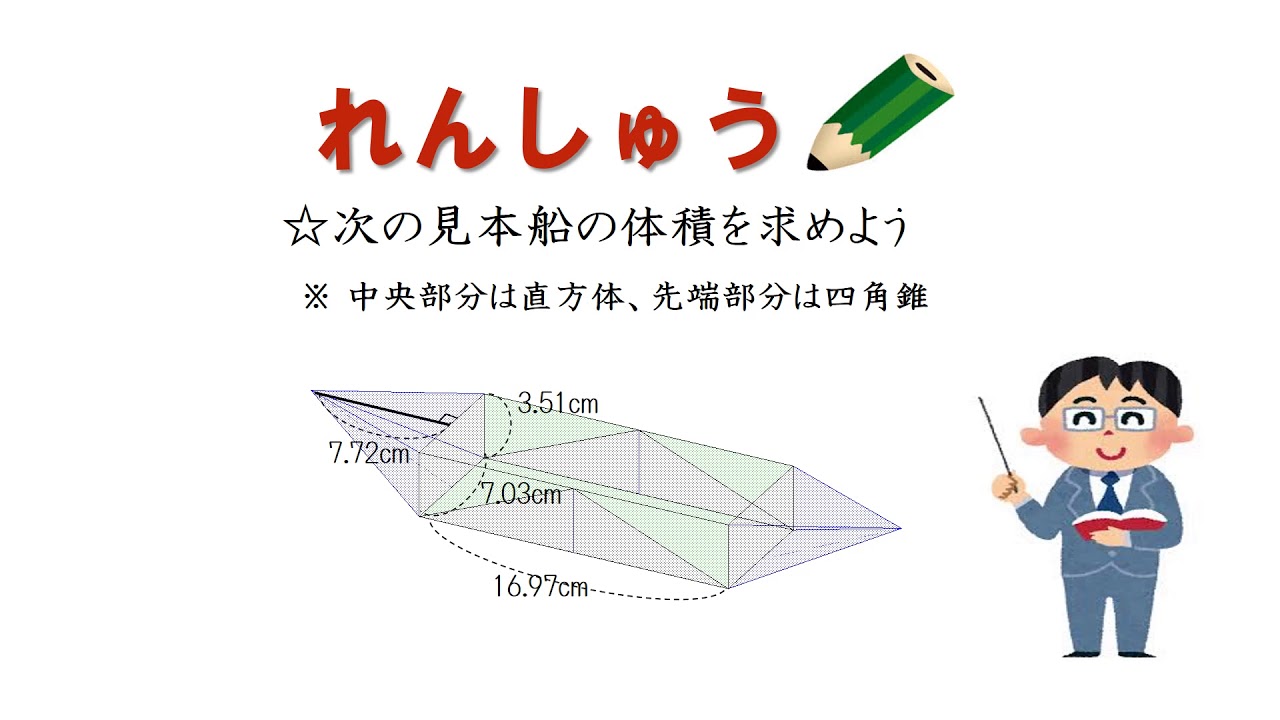


中学校数学科おりがみ見本船の体積の求め方 Youtube


年の最高 五角柱の体積の求め方 幼児 小学生 中学生の無料知育教材 無料学習教材プリント


2
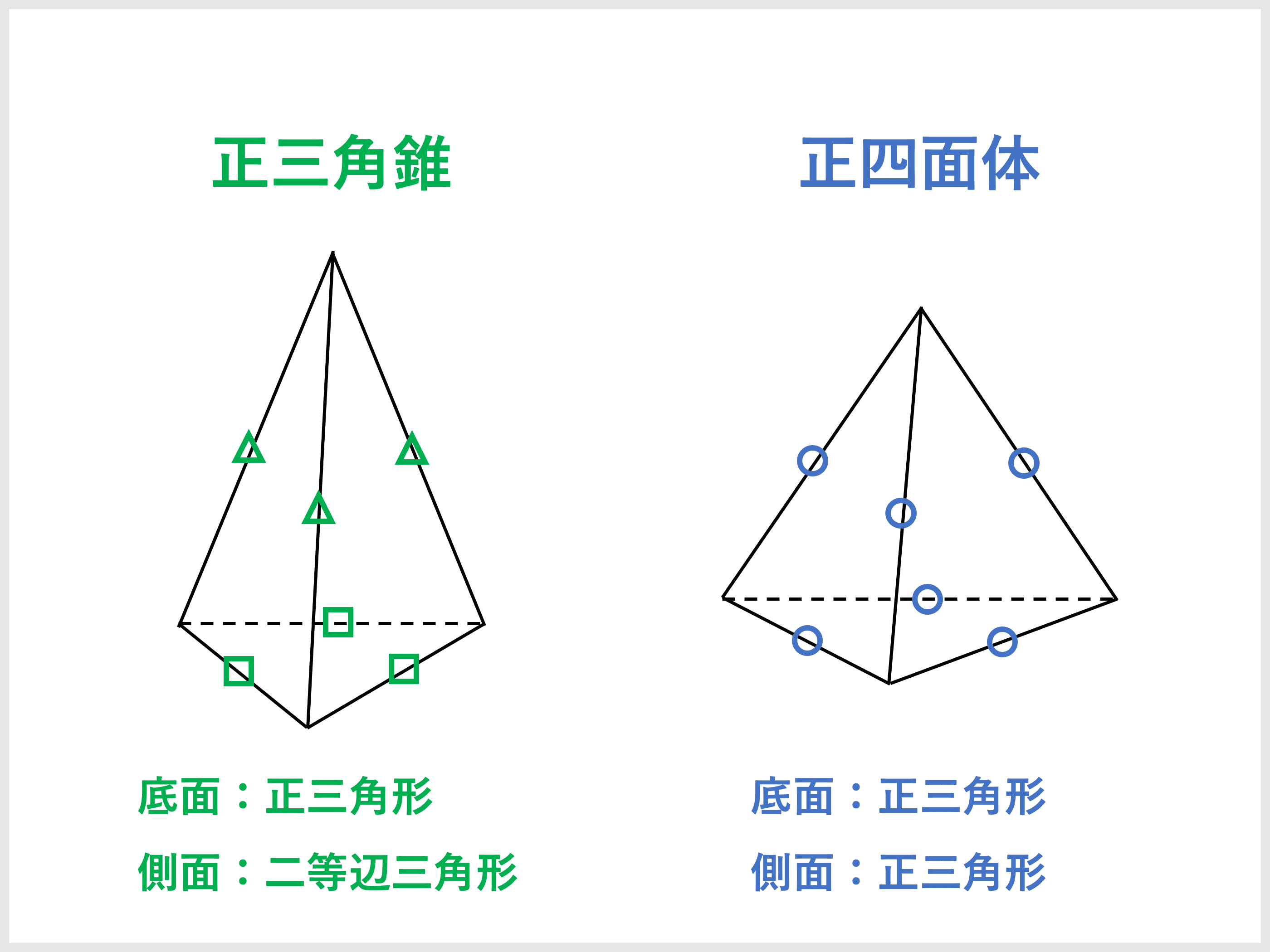


三角錐とは 体積 表面積の公式や求め方 受験辞典



ট ইট র Kato 少なくとも 三角比の公式を覚えておけば立体になっても計算は変わらない 三角比の勉強が 数1では大事だなぁ チーム エン 岐阜県各務原市の個別総合塾 三平方の定理の利用 四角錐 円錐 T Co Xvpgc6ihgw T Co Vy93bckkbi



計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく


花まるラボ スマホやタブレットで使える中学受験対策アプリ 究極の立体 展開 を発売 Edtechzine エドテックジン



角錐 Pyramid Geometry Japaneseclass Jp


Http Kanra Schoolnet Ed Jp Obatasho Action Common Download Main Upload Id 677


簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者


回答 点pが動く四角錐の体積を求める 空間図形 数塾ブログ



3分でわかる 円錐の体積 表面積の求め方 合格サプリ


面積と体積公式の覚え方と長い式を書く練習 公開 学友舎 Lab サブサイト


四角錐 Wikipedia


2
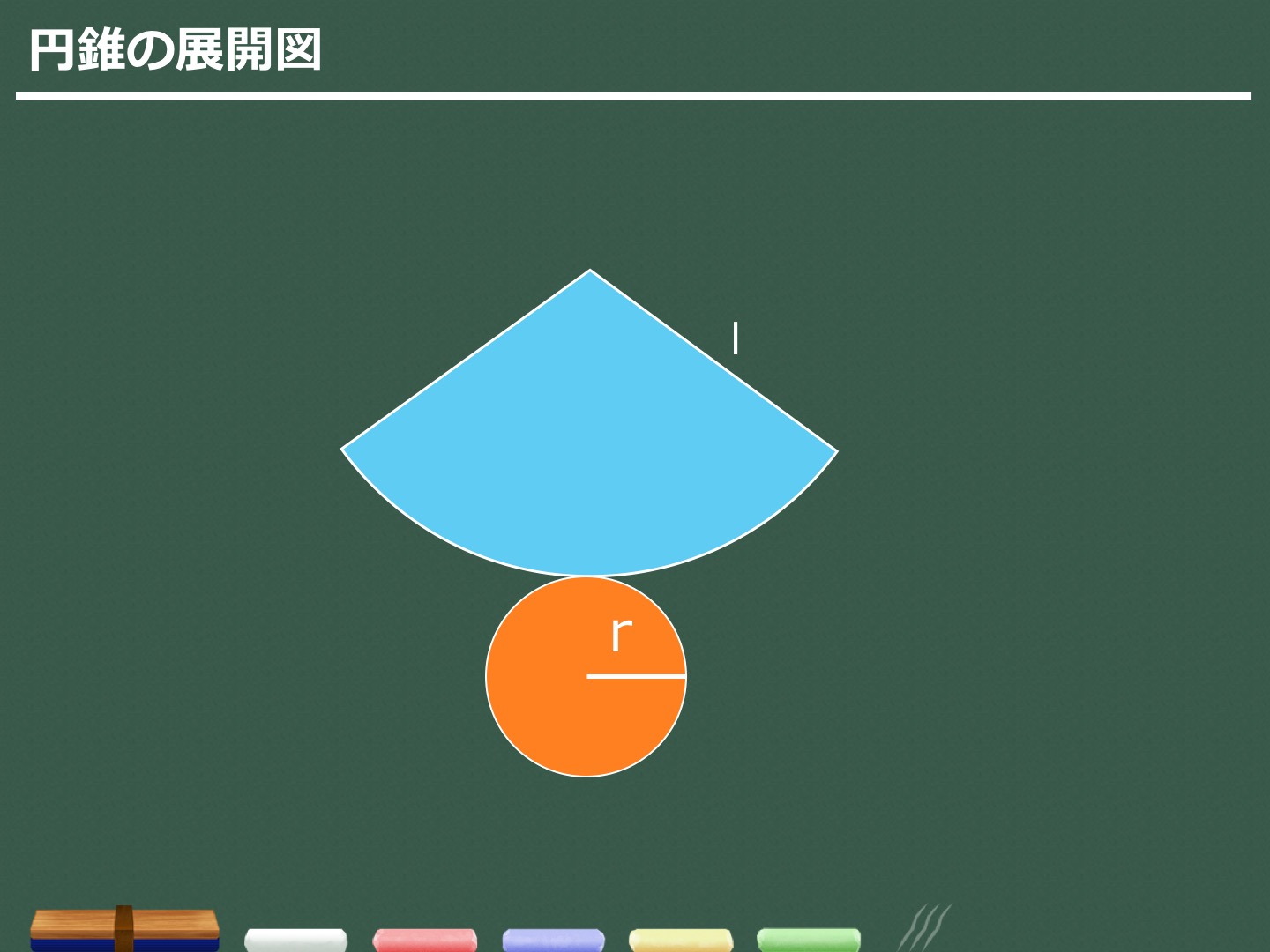


3分でわかる 円錐の体積 表面積の求め方 合格サプリ



円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ



相似な図形の問題です 中学数学に関する質問 勉強質問サイト



心に強く訴える角錐体積公式 ただぬりえ



中2数学 中学数学に関する質問 勉強質問サイト



中1数学047 空間図形 体積と表面積 角柱と角錐 体積は公式 表面積は展開図を書いて楽勝だ Youtube


シンプソンの公式 応用編 Fukusukeの数学めも



中3 三角形の相似 四角錐の体積比 日本語版 Youtube
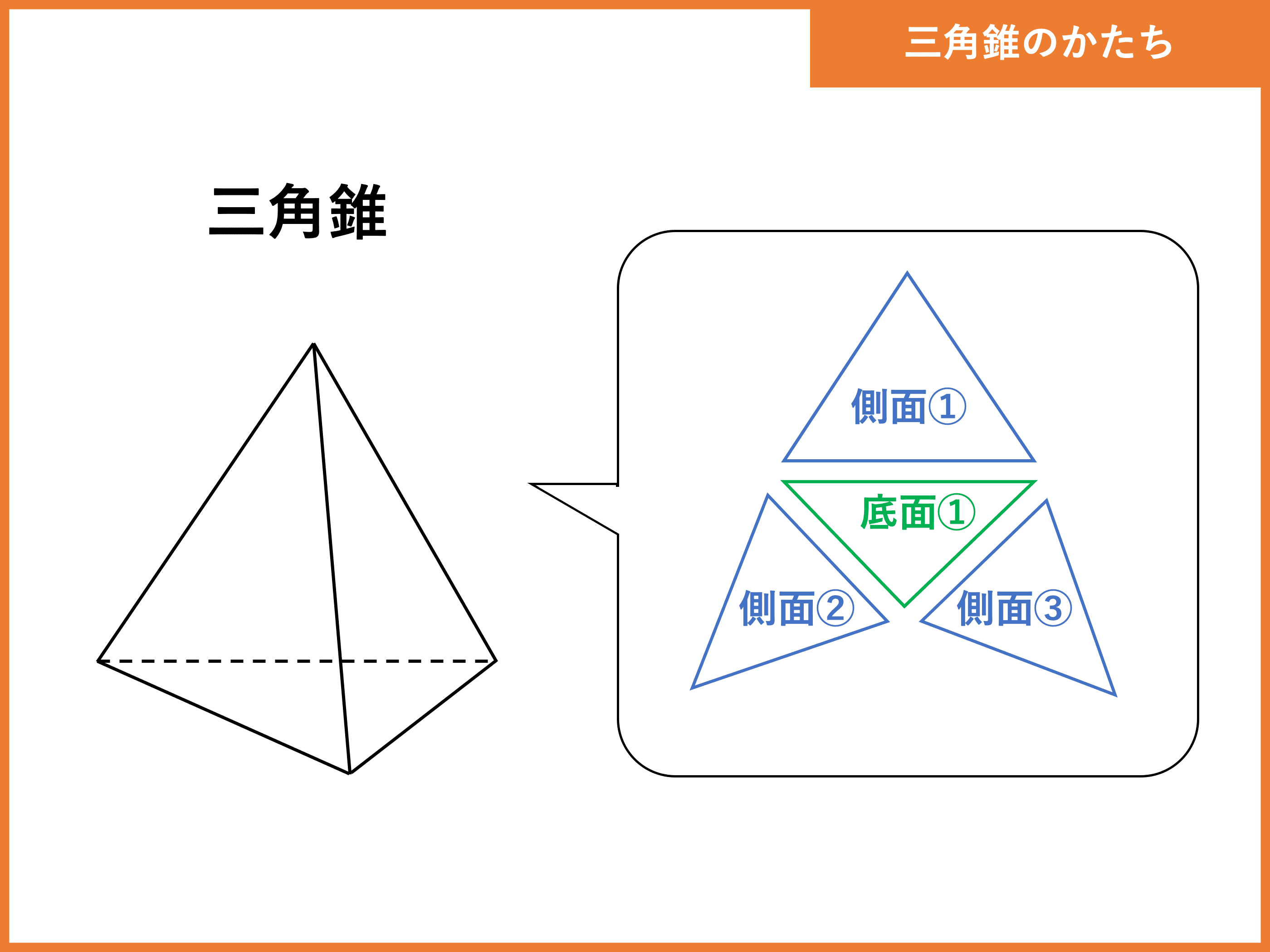


三角錐とは 体積 表面積の公式や求め方 受験辞典



中学2年生です Clear



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



高みき そろばん先生 東大生 中3受験生に夏休みの間毎日2時間数学教えてるんだけど これ解くのに 柱と錐の違い 錐の体積の出し方 正方形の面積の公式 三角形の面積の公式 が何ひとつわかってなくて教えてるこっちがキツかった とりあえず掛け算



0 件のコメント:
コメントを投稿